Descripción
Los algoritmos de clustering son muy populares porque se pueden aplicar a datos supervisados y no supervisados para entender mejor su naturaleza y descubrir cualquier estructura interna que permita agruparlos y describirlos de acuerdo con algún criterio. Básicamente, se trata de particionar el conjunto de datos en k subgrupos disjuntos de manera que obtenemos una clasificación de los datos según su naturaleza, la cual esperamos que nos revele alguna información de ellos.
El problema principal de muchos algoritmos de clustering es que hay que elegir el número de clústeres k para decidir en cuántos subgrupos se puede partir un conjunto de datos de manera óptima, teniendo en cuenta la naturaleza del problema que se quiere resolver, pero también el algoritmo de clustering elegido.
Se han desarrollado muchos indicadores que nos dicen lo buena que es una solución basada en k clústeres. La mayoría tienen en cuenta aspectos geométricos, por ejemplo, si los clústeres son esféricos, si están muy separados, etc. Desgraciadamente, no hay un criterio mejor que los otros y todo depende de la naturaleza de los datos, y también de si tenemos alguna idea respecto al número de clústeres que esperamos encontrar. Lo que se hace habitualmente es probar diferentes valores de k en un rango y decidir cuál es el óptimo de acuerdo con un indicador elegido a priori. Hemos cambiado la cuestión, ¡de tener que elegir k, ahora tenemos que elegir el indicador adecuado! Además, para conjuntos de datos grandes y rangos de k grandes, el tiempo de computación puede ser muy elevado.
El problema es que para el mismo algoritmo y el mismo conjunto de datos, diferentes indicadores o criterios para elegir k proporcionan resultados distintos, así pues, no hay ninguna manera de asegurar que hemos encontrado el óptimo. Sin embargo, si la mayoría de indicadores coinciden en un mismo valor de k y la solución encontrada nos parece adecuada para el problema que queremos resolver, ello puede servirnos de ayuda. Esto es lo que hace el paquete NbClust de R, que permite automatizar el proceso para una treintena de indicadores distintos.
Enlace al recurso
https://en.wikipedia.org/wiki/Determining_the_number_of_clusters_in_a_data_set
Ejemplo de uso
La siguiente figura muestra el resultado del algoritmo k-means sobre un conjunto de datos denominado Cassini para tres clústeres; podéis probar diferentes conjuntos de datos y número de clústeres para ver el resultado obtenido.
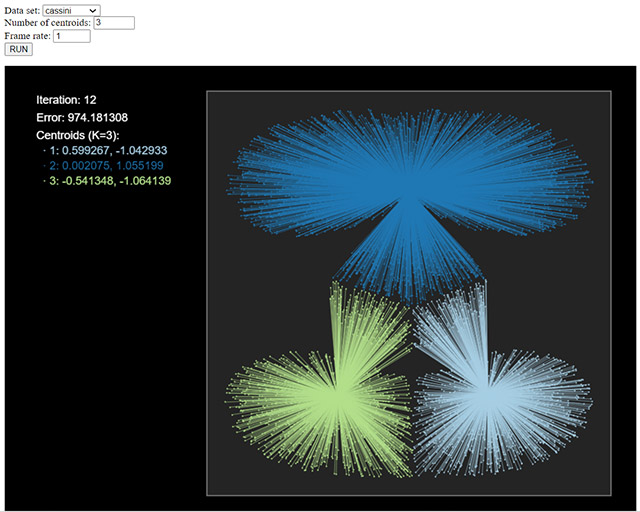
En este caso, el indicador elegido es el error cuadrático mediano, y deberíamos explorar diferentes valores de k para ver cómo evoluciona y decidir el valor óptimo de k (¡si es que existe!). Podéis probarlo usando el paquete NbClust, variante k entre 1 y 10, por ejemplo.
En la asignatura Minería de datos del grado de Ciencia de Datos Aplicada de la UOC tendréis que aplicar técnicas similares para decidir el número de clústeres cuando aplicáis algoritmos de clustering.
Enlaces relacionados
El paquete de R NbClust: https://cran.r-project.org/web/packages/NbClust/index.html
Algoritmo k-means en línea: http://personal.uoc.edu/opendataviz/kmeans/kmeans.html
