Descripción
El equilibrio entre sesgo y varianza (en inglés bias-variance tradeoff) es un concepto muy importante que nos ayuda a entender lo bueno que es un modelo estadístico o de minería de datos cuando se enfrenta a datos que no se han usado para entrenarlo, es decir, lo bien que generaliza.
Cuando se crea un modelo, normalmente los datos disponibles se separan en dos conjuntos: uno de entrenamiento y otro de test. El modelo se crea con el conjunto de entrenamiento y se evalúa con el conjunto de test, y generalmente se obtienen peores resultados, pero se espera que el algoritmo generalice mejor cuando se use con datos nuevos. El error cometido depende de la naturaleza del problema, del algoritmo empleado y de la «calidad» del conjunto de datos, entendiendo por «calidad» el hecho de ser representativo del problema que quiere resolverse, la cantidad de muestras, si no hay sesgos, cómo se ha partido en el conjunto de entrenamiento y en el de test, etc.
El error de nuestro modelo se ve, pues, como la suma de un error de sesgo a causa de la pobreza de nuestro algoritmo al capturar la esencia del problema, más un error de varianza causado por las variaciones posibles en el conjunto de entrenamiento, más un error desconocido que depende de la naturaleza del problema que estamos resolviendo, que se considera no tratable. Los errores de sesgo y de varianza son contrapuestos; modelos que resuelvan muy bien el problema (por ejemplo, un árbol de decisión lo bastante grande para clasificar el conjunto de entrenamiento perfectamente) tendrán un error de sesgo cero, pero serán muy sensibles al conjunto de entrenamiento y tendrán un error de varianza elevado, por eso se habla de equilibrio o tradeoff. Idealmente, queremos un modelo con un error de sesgo y de varianza limitado, tal y como muestra la siguiente figura:
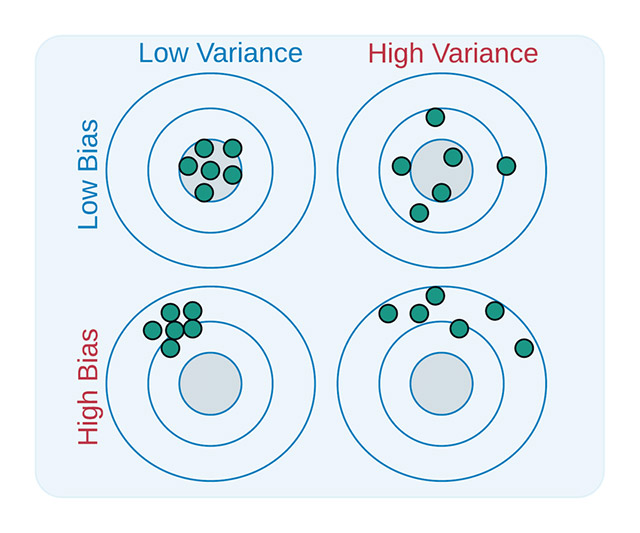
Por lo tanto, si nuestro modelo «apunta» a la diana, nos interesa que todos los rasgos (las predicciones) estén centradas y agrupadas (poco sesgo y poca varianza). Para saber lo bueno que es nuestro modelo, se hacen simulaciones generando diferentes conjuntos de entrenamiento y midiendo el error de cada modelo parcial construido, descomponiéndolo en un sesgo y una varianza, lo que nos puede permitir (en parte) saber si tenemos un modelo muy apuntado hacia nuestro objetivo, o bien si no tenemos los datos adecuados para entrenarlo correctamente.
Enlace al recurso
https://mlu-explain.github.io/bias-variance/
Ejemplo de uso
El enlace proporcionado conduce a un recurso en línea dinámico que muestra el concepto equilibrio entre sesgo y varianza usando un modelo de regresión como ejemplo. Primero utiliza un modelo sencillo, lineal, que no ajusta bien los datos del conjunto de entrenamiento y con un error de sesgo elevado. Después utiliza un modelo más complejo, con un polinomio ajustado a los datos de entrenamiento y que tiene un error de sesgo 0, pero que generaliza muy mal.
Para medir el error de varianza se generan distintos conjuntos de entrenamiento al azar, se miden los dos modelos y se obtienen curvas diferentes:
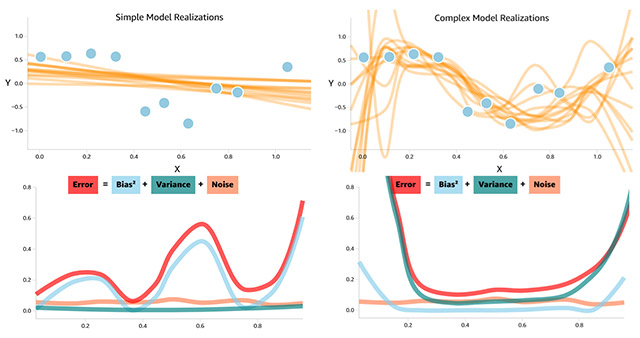
A la izquierda el modelo simple y, a la derecha, el complejo
Cómo se puede ver, el error total es diferente para los dos casos: uno está causado por el sesgo y el otro está causado por la varianza. Por lo tanto, deberemos ajustar nuestro modelo para que no sea muy sencillo y capture bien la naturaleza de los datos, pero que continúe generalizando bien.
Aunque se trata de un concepto avanzado, os puede ser útil cuando construyáis y evaluéis modelos en distintas asignaturas del grado de Ciencia de Datos Aplicada de la UOC.
Enlaces relacionados
Entrada en la Wikipedia: https://en.wikipedia.org/wiki/Bias-variance_tradeoff
Ejemplo en R: https://statisticallearning.org/bias-variance-tradeoff.html
