Descripción
La siguiente imagen, creada por Thomas Lumley (@tslumley), muestra todas las posibles combinaciones entre dos o más variables que pueden explicar la correlación entre dos variables, sin que ello implique que una variable es la causa de la otra. Obviamente, una correlación elevada entre dos variables indica que hay cierta asociación entre ambas, pero no quiere decir que una variable sea la única causa que explica la otra.
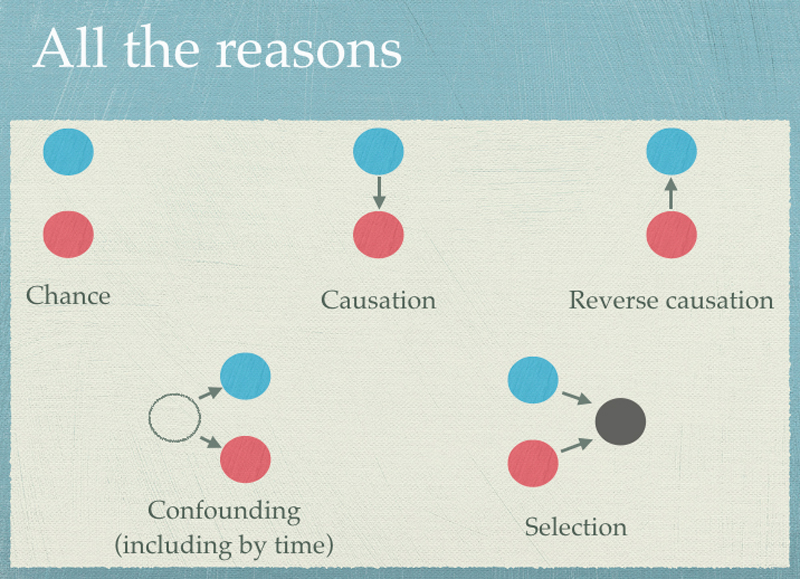
Así, dos variables pueden estar correlacionadas, pero pueden darse los casos siguientes:
- Se puede deber al azar y no existir ninguna relación entre variables. Es lo que se conoce como una correlación espuria.
- Puede ser que las variables sí que estén relacionadas entre sí y que una sea la causa y la otra, el efecto. En función de cómo de lineal sea dicha relación, la correlación medida será más o menos elevada.
- Puede existir una variable que sea la causa de las otras dos variables. Por ejemplo, los hechos «llevar paraguas» y «llevar botas de agua» seguramente están correlacionados pero están causados por un tercer hecho «está lloviendo».
- Puede que ambas variables estén condicionadas por una selección de casos creada por otra variable. Por ejemplo, si para ir a una fiesta los hombres deben disfrazarse, sería posible encontrar una correlación elevada entre «va disfrazado» y «es un hombre», lo cual no sería extrapolable fuera de la selección causada por el hecho de estar en la fiesta.
Enlace al recurso
https://twitter.com/tslumley/status/1125661624356954112
Enlaces relacionados
Correlación: https://es.wikipedia.org/wiki/Correlación
Spurious correlations: https://tylervigen.com/spurious-correlations
Cum hoc ergo propter hoc: https://es.wikipedia.org/wiki/Cum_hoc_ergo_propter_hoc