Descripción
La paradoja de Simpson, también llamada efecto de Yule-Simpson, consiste en la desaparición o inversión de una relación entre diferentes variables cuando los datos se agrupan de forma diferente, en función de otra variable no considerada previamente. Aunque otros autores habían mencionado el efecto anteriormente, fue Simpson el primero que publicó un trabajo de carácter técnico en el que la describía.
Simpson, Edward H. (1951). «The Interpretation of Interaction in Contingency Tables». Journal of the Royal Statistical Society, Series B (vol. 13, núm. 2, págs. 238-241).
La idea básica es que incluso una correlación elevada encontrada entre dos variables puede ser interpretada erróneamente, si una tercera variable usada para separar en grupos los datos analizados conlleva implícita otra asociación que puede ser también relevante, pero de signo contrario. Por lo tanto, el orden de selección de variables cuando se analizan correlaciones es importante y, como siempre, una inspección visual previa de los datos puede ser de ayuda.
Enlace al recurso
https://en.wikipedia.org/wiki/Simpson%27s_paradox
Ejemplo de uso
La paradoja de Simpson es más fácil de entender mediante una visualización de datos como la siguiente. Si se considera todo el conjunto de datos, se obtiene una correlación negativa entre las dos variables representadas de –0,74, la cual se puede percibir a simple vista. Pero si se consideran los grupos determinados por una tercera variable, se puede observar que, para cada grupo, la correlación obtenida para cada uno de ellos tiene una magnitud parecida, pero de signo contrario.
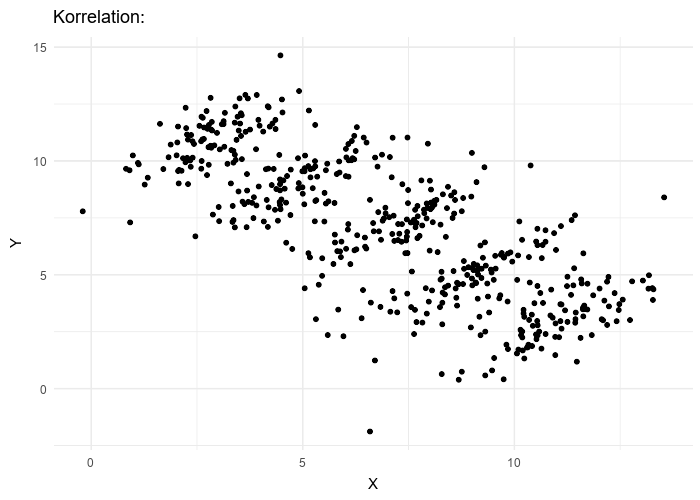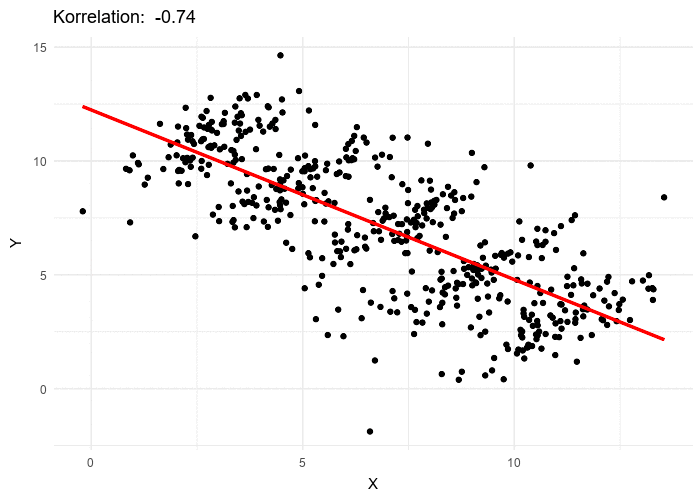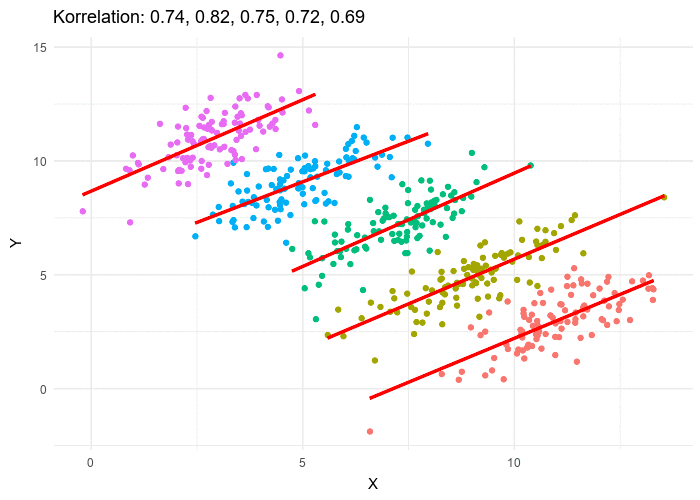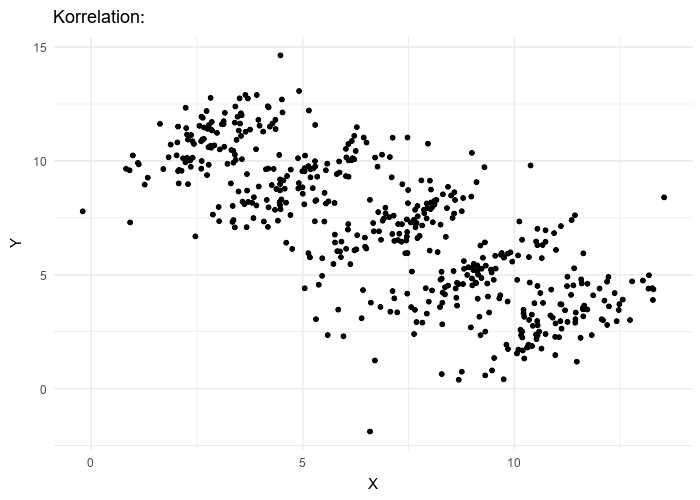Fuente: https://commons.wikimedia.org/wiki/File:Simpsons_paradox_-_animation.gif
Enlaces relacionados
Beyond Simpson’s Paradox: One problem in Data Science: https://link.springer.com/chapter/10.1007/978-3-642-72253-0_9
Ejemplo de las admisiones en UC Berkeley por género: https://www.r-bloggers.com/simpsons-paradox-is-back/