Descripción
Un diagrama de Voronoi es una partición del espacio (habitualmente 2D) en regiones, generada a partir de una colección de puntos que representan los centros (en un sentido figurado) de cada región, de forma que todos los puntos que pertenecen a una misma región están más cercanos a su centro que a ningún otro centro.
En sentido geométrico, basado en una función distancia, el diagrama de Voronoi establece los límites de las áreas de influencia del punto utilizado como centro de cada área, de forma que para un punto cualquiera se puede saber a qué área pertenece y qué centro es el más cercano, según la función distancia escogida, que típicamente es la euclídea, la cual genera regiones convexas.
Por ejemplo, si calculamos el diagrama de Voronoi usando como centros las capitales de provincia en España, obtenemos un resultado bastante sorprendente:
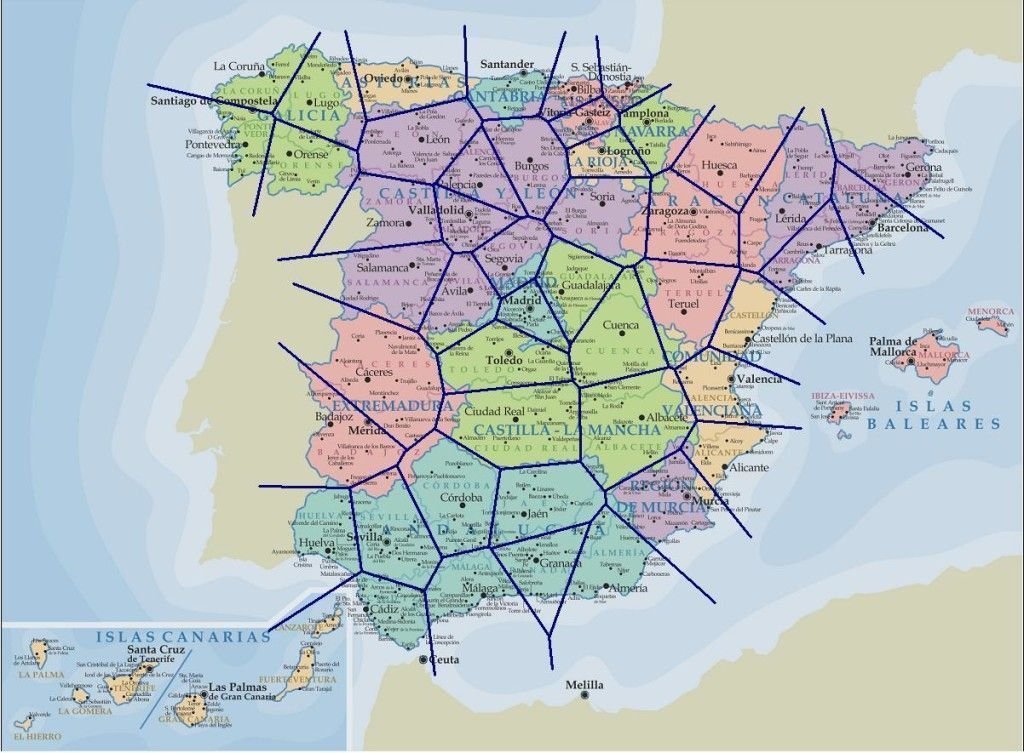
Diagrama de Voronoi superpuesto a un mapa provincial de España. Fuente: https://www.geografiainfinita.com/2014/05/el-mundo-perfecto-de-voronoi-donde-matematica-y-geografia-se-unen/
Como se puede ver, las regiones creadas por el diagrama de Voronoi se superponen razonablemente bien con las provincias. Esto no es casualidad, sino que refleja el criterio usado por Javier de Burgos en 1833 para crear dicha división administrativa. De Burgos buscaba que desde el punto más alejado de la provincia se pudiera llegar a la capital en un día de viaje como máximo, por lo que la división en provincias lleva implícita una función distancia.
Enlace al recurso
https://en.wikipedia.org/wiki/Voronoi_diagram
Ejemplo de uso
Supongamos que queremos analizar si la distribución de un cierto recurso está bien repartida por un área. Por ejemplo, queremos saber cómo están distribuidas las farmacias de la ciudad de Barcelona y si, más o menos, cubren áreas de influencia similares en tamaño y distancia al centro. A partir de las posiciones geolocalizadas de cada farmacia podemos generar un diagrama de Voronoi tratándolas como los centros de cada región, y podemos superponer el diagrama resultante a un mapa para ver su distribución espacial.
La lista de farmacias de Barcelona y su posición geolocalizada la podemos obtener, por ejemplo, de un fichero de datos abiertos que publica la Generalitat de Catalunya. Tras un procesamiento para resolver los problemas detectados (un ejercicio interesante), supongamos que tenemos un fichero con los datos de las farmacias de Barcelona ciudad. Entonces podemos generar un diagrama de Voronoi en R y superponerlo a un mapa generado con leaflet también desde R:
require(leaflet)
require(ggvoronoi)
// contiene al menos los campos NOMBRE, LONGITUD y LATITUD
x=read.table("farmacias.csv", sep=";", header=T, quote="")
// eliminar puntos repetidos o sin geolocalización
xxi=unique(x[x$LONGITUD!=0 & x$LATITUD!=0, c(‘LONGITUD’,’LATITUD’)])
xx=x[rownames(xxi),]
// crear el mapa
mapa=leaflet()
mapa=addTiles(mapa,
urlTemplate = "http://{s}.tile.openstreetmap.org/{z}/{x}/{y}.png")
// crear el diagrama de Voronoi
vvv=voronoi_polygon(xx, x='LONGITUD', y='LATITUD')
// añadir los centros al mapa
mapa=addMarkers(mapa, lng=vvv$LONGITUD, lat=vvv$LATITUD, popup=vvv$NOMBRE)
// añadir los polígonos generados por el diagrama de Voronoi
mapa=addPolygons(mapa, data=vvv)
// mostrar el mapa
mapa
La visualización de la variable mapa abrirá una ventana del navegador por defecto y mostrará un mapa como el siguiente (una vez ajustado el zum):
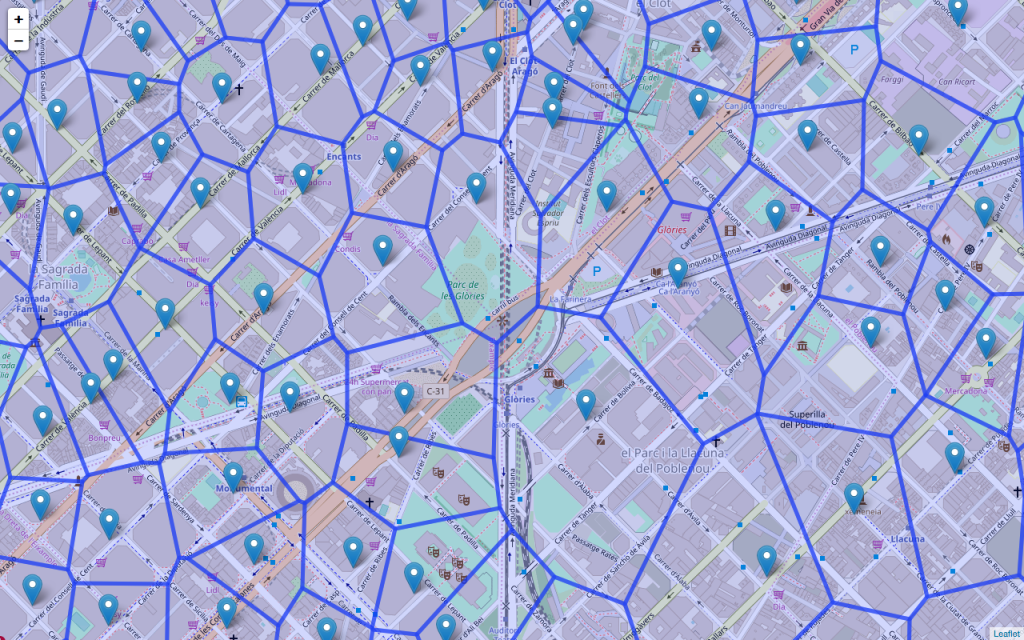
Como se puede ver, para cada farmacia se ha encontrado su área de influencia, aunque al usar la distancia euclídea por defecto las regiones creadas por el diagrama de Voronoi no siguen ningún patrón relativo a la estructura de calles, que es cuadriculada. No obstante, el diagrama permite comprobar que hay zonas con una gran densidad de farmacias, mientras que hay otras zonas donde una farmacia cubre más territorio, seguramente siguiendo un patrón relacionado con la densidad de población (este sería otro ejercicio interesante).
Enlaces relacionados
En Mathematica: http://mathworld.wolfram.com/VoronoiDiagram.html
Leaflet para R: https://rstudio.github.io/leaflet/
El package ggvoronoi de R: https://cran.r-project.org/web/packages/ggvoronoi/index.html
Diagrama de Voronoi superpuesto a un mapa provincial de España: https://www.geografiainfinita.com/2014/05/el-mundo-perfecto-de-voronoi-donde-matematica-y-geografia-se-unen/