Descripción
Cuando analizamos redes (o grafos), lo más habitual es empezar por describir los estadísticos más sencillos relacionados con los elementos de la red, es decir, nodos y arcos o aristas (dependiendo de si la red o el grafo está dirigido o no, respectivamente). Entre otros, se pueden calcular los siguientes descriptores de manera sencilla:
- el número de nodos,
- el número de arcos o aristas,
- la densidad, que es el número de arcos o aristas dividido por el número total que podría contener la red si fuera completa, y
- el grado en término medio.
Obviamente, hay otros descriptores más sofisticados que pueden aportar información sobre la estructura interna de la red, pero son más complicados de calcular y de interpretar.
Enlace al recurso
https://zenodo.org/record/5083036
Ejemplo de uso
La siguiente figura, creada por Martin Grandjean (@GrandjeanMartin en Twitter), muestra como cuatro redes absolutamente diferentes pueden compartir los mismos descriptores, igual que sucede con el ejemplo del cuarteto de Anscombe. Por lo tanto, es importante visualizar los datos (en este caso, la red) para poder captar la naturaleza real más allá de estos descriptores, puesto que dos redes que comparten el mismo número de nodos y la misma distribución de grados pueden ser completamente distintas.
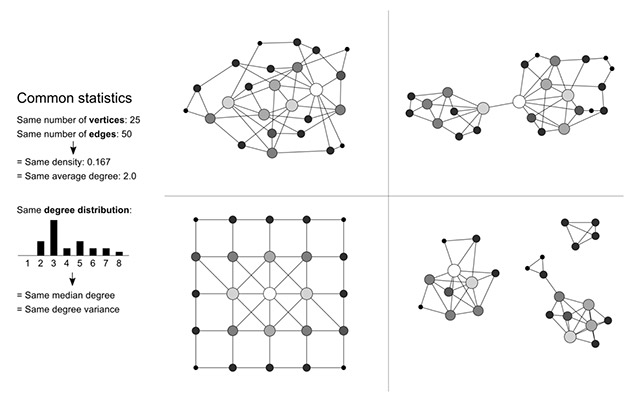
Pero atención, la visualización también puede ser mal interpretada si no se tiene en cuenta que dos redes idénticas (mejor dicho, isomorfas) pueden representarse de manera diferente, en función de donde se sitúen sus elementos, como sucede en el caso de las redes superior izquierda e inferior izquierda. Desgraciadamente, saber si dos redes son isomorfas es un problema complicado de resolver para redes de cierta medida.
Ejemplos como este se estudian en la asignatura Análisis de redes sociales del grado de Ciencia de Datos Aplicada de la UOC.
Enllaços relacionats
Cuarteto de Anscombe: https://es.wikipedia.org/wiki/Cuarteto_de_Anscombe
Grafos isomorfos: https://en.wikipedia.org/wiki/Graph_isomorphism_problem
