Descripció
Els algorismes de clústering són molt populars perquè es poden aplicar a dades supervisades i no supervisades, per entendre’n més bé la seva naturalesa i descobrir qualsevol estructura interna que permeti agrupar-les i descriure-les d’acord amb algun criteri. Bàsicament, es tracta de particionar el conjunt de dades en k subgrups disjunts de manera que obtenim una classificació de les dades d’acord amb la seva naturalesa que esperem que ens en reveli alguna informació.
El problema principal de molts algorismes de clústering és que cal triar el nombre de clústers k per decidir en quants subgrups es pot partir un conjunt de dades de manera òptima, tenint en compte la naturalesa del problema que es vol resoldre, però també l’algorisme de clústering triat.
S’han desenvolupat molts indicadors que ens diuen com és de bona una solució basada en k clústers. La majoria tenen en compte aspectes geomètrics, per exemple, si els clústers són esfèrics, estan ben separats, etc. Malauradament, no hi ha un criteri millor que els altres, tot depèn de la naturalesa de les dades, i també de si tenim alguna idea respecte al nombre de clústers que esperem trobar. El que es fa habitualment és provar diferents valors de k en un rang i decidir quin és el valor de k òptim d’acord amb un indicador triat a priori. Hem canviat la qüestió, d’haver de triar k ara hem de triar l’indicador adequat! A més, per a conjunts de dades grans i rangs de k grans el temps de computació pot ser molt elevat.
El problema és que per al mateix algorisme i el mateix conjunt de dades, diferents indicadors o criteris per triar k proporcionen resultats diferents, així doncs, no hi ha cap manera d’assegurar que hem trobat l’òptim. Ara, si la majoria d’indicadors coincideixen en un mateix valor de k i la solució trobada ens sembla adequada per al problema que volem resoldre, doncs ens pot servir d’ajuda. Això és el que fa el paquet NbClust d’R, que ens permet automatitzar això per a una trentena d’indicadors diferents.
Enllaç al recurs
https://en.wikipedia.org/wiki/Determining_the_number_of_clusters_in_a_data_set
Exemple d’ús
La figura següent mostra el resultat de l’algorisme k-means sobre un conjunt de dades anomenat Cassini per a tres clústers, podeu provar diferents conjunts de dades i nombre de clústers per veure el resultat obtingut.
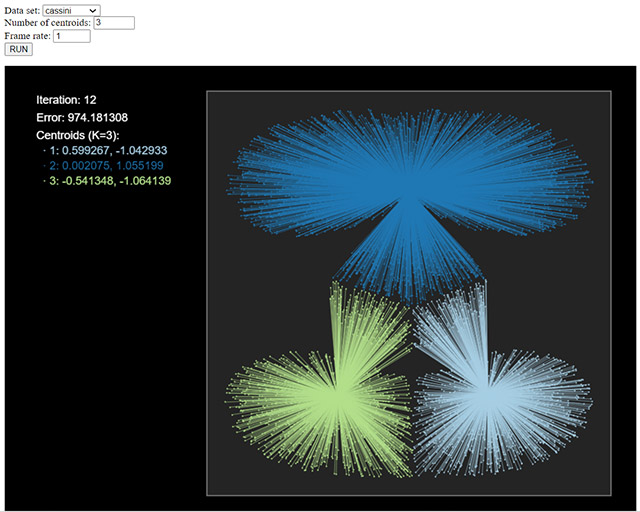
En aquest cas, l’indicador triat és l’error quadràtic mitjà, i hauríem d’explorar diferents valors de k per veure com evoluciona, per decidir el valor òptim de k (si és que existeix!). Podeu provar-ho fent servir el paquet NbClust, variant k entre 1 i 10, per exemple.
A l’assignatura Mineria de dades, del grau de Ciència de Dades Aplicada, de la UOC, haureu d’aplicar tècniques similars per decidir el nombre de clústers quan apliqueu algorismes de clústering.
Enllaços relacionats
El paquet d’R NbClust: https://cran.r-project.org/web/packages/NbClust/index.html
Algorisme k-means en línia: http://personal.uoc.edu/opendataviz/kmeans/kmeans.html
