Descripció
L’equilibri entre biaix i variància (en anglès bias-variance tradeoff) és un concepte molt important que ens ajuda a entendre com és de bo un model estadístic o de mineria de dades quan s’enfronta a dades que no s’han fet servir per entrenar-lo, és a dir, com de bé generalitza.
Quan es crea un model, normalment les dades disponibles se separen en dos conjunts, un d’entrenament i un de test. El model es crea amb el conjunt d’entrenament i s’avalua amb el conjunt de test, generalment s’obtenen més mal resultats, però s’espera que l’algorisme generalitzi millor quan es faci servir amb dades noves. L’error comès depèn de la naturalesa del problema, de l’algorisme emprat i de la «qualitat» del conjunt de dades, entenent per qualitat el fet de ser representatiu del problema que es vol resoldre, la quantitat de mostres, si no hi ha biaixos, com s’ha partit en el conjunt d’entrenament i el de test, etc.
L’error del nostre model es veu, doncs, com la suma d’un error de biaix a causa de la pobresa del nostre algorisme en capturar l’essència del problema, més un error de variància causat per les variacions possibles en el conjunt d’entrenament, més un error desconegut que depèn de la naturalesa del problema que estem resolent, que es considera no tractable. Els errors de biaix i de variància són contraposats, models que resolguin molt bé el problema (per exemple, un arbre de decisió prou gran per classificar el conjunt d’entrenament perfectament) tindran un error de biaix zero, però seran molt sensibles al conjunt d’entrenament i tindran un error de variància elevat, per això es parla d’equilibri o tradeoff. Idealment, volem un model amb un error de biaix i de variància limitats, tal com mostra la figura següent:
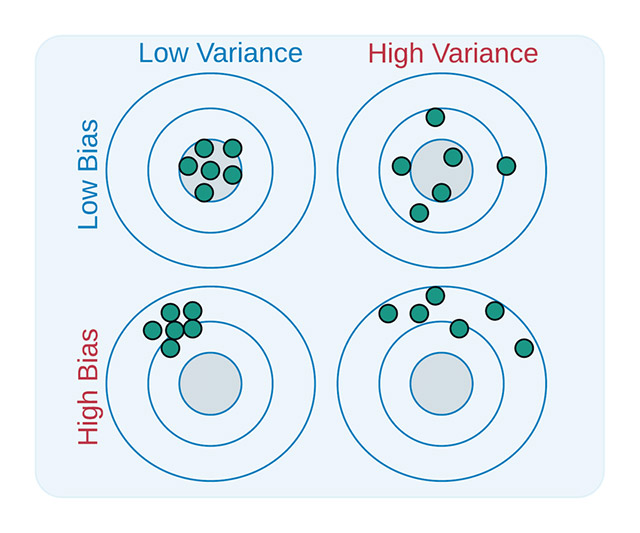
És a dir, si el nostre model «apunta» a la diana, ens interessa que tots els trets (les prediccions) siguin centrades i agrupades (poc biaix i poca variància). Per saber com és de bo el nostre model, es fan simulacions generant diferents conjunts d’entrenament i mesurant l’error de cada model parcial construït, descomponent-lo en un biaix i una variància, cosa que ens pot permetre (en part) saber si tenim un model ben apuntat cap al nostre objectiu o bé si no tenim les dades adequades per entrenar-lo correctament.
Enllaç al recurs
https://mlu-explain.github.io/bias-variance/
Exemple d’ús
L’enllaç proporcionat porta a un recurs en línia dinàmic que mostra el concepte d’equilibri entre biaix i variància, fent servir un model de regressió com a exemple. Primer utilitza un model senzill, lineal, que no ajusta bé les dades del conjunt d’entrenament, amb un error de biaix elevat. Després utilitza un model més complex, amb un polinomi ajustat a les dades d’entrenament, que té un error de biaix 0, però que generalitza molt malament.
Per mesurar l’error de variància es generen diferents conjunts d’entrenament a l’atzar i es mesuren els dos models, i s’obtenen corbes diferents:
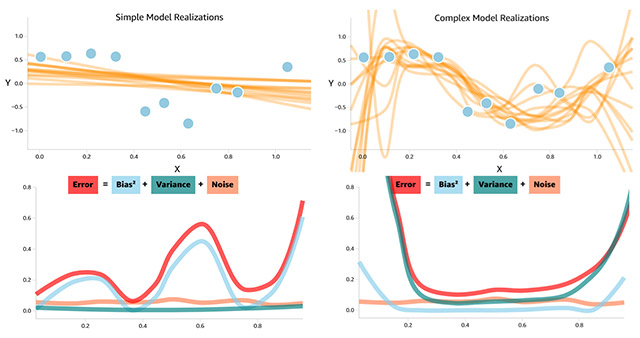
A l’esquerra el model simple, i a la dreta, el complex.
Com es pot veure, l’error total és diferent per als dos casos, un causat pel biaix i l’altre causat per la variància. Per tant, haurem d’ajustar el nostre model perquè no sigui gaire senzill, i capturi bé la natura de les dades, però continuï generalitzant bé.
Tot i que es tracta d’un concepte avançat, us pot ser útil quan construïu i avalueu models en diferents assignatures del grau de Ciència de Dades Aplicada de la UOC.
Enllaços relacionats
Entrada a la Wikipedia: https://en.wikipedia.org/wiki/Bias-variance_tradeoff
Exemple en R: https://statisticallearning.org/bias-variance-tradeoff.html
