Descripció
Un diagrama de Voronoi és una partició de l’espai (habitualment 2D) en regions, generada a partir d’una col·lecció de punts que representen els centres (en un sentit figurat) de cada regió, de manera que tots els punts que pertanyen a una mateixa regió estan més propers al seu centre que a cap altre centre.
En sentit geomètric, basat en una funció distància, el diagrama de Voronoi estableix els límits de les àrees d’influència del punt utilitzat com a centre de cada àrea, de manera que per a un punt qualsevol es pot saber a quina àrea pertany i quin centre és el més proper, segons la funció distància escollida, que típicament és l’euclidiana, la qual genera regions convexes.
Per exemple, si calculem el diagrama de Voronoi usant com a centres les capitals de província a Espanya, obtenim un resultat bastant sorprenent:
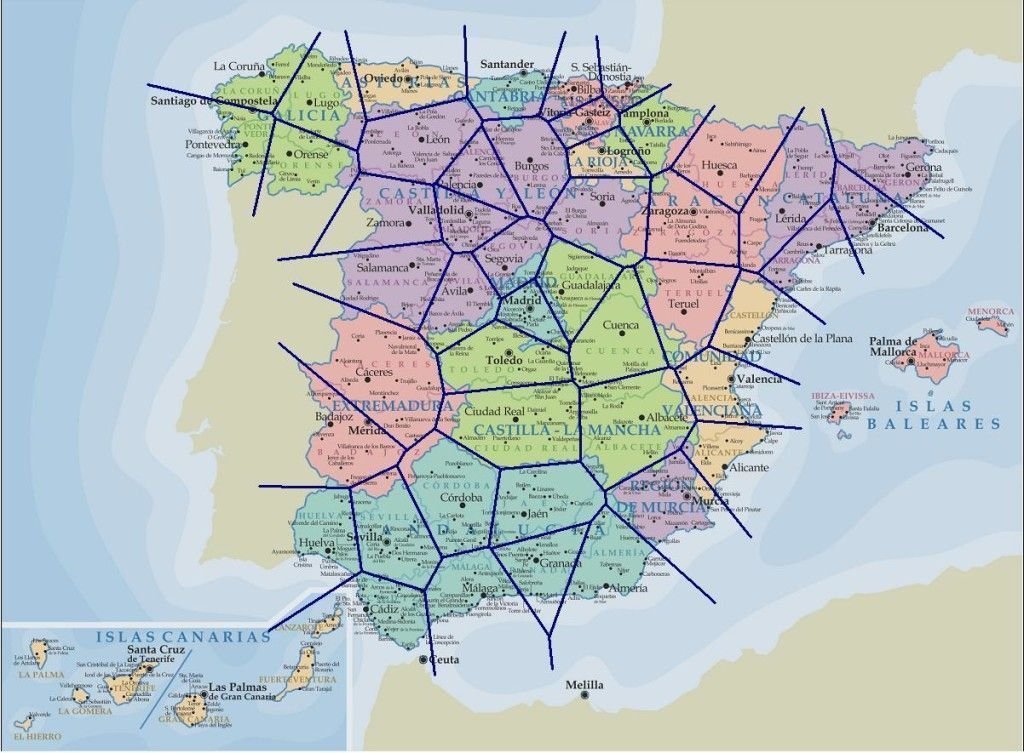
Com es pot veure, les regions creades pel diagrama de Voronoi se superposen raonablement bé amb les províncies. No és casualitat, sinó que reflecteix el criteri usat per Javier de Burgos el 1833 per a crear aquesta divisió administrativa. De Burgos buscava que des del punt més allunyat de la província es pogués arribar a la capital en un dia de viatge com a màxim, per la qual cosa la divisió en províncies porta implícita una funció distància.
Enllaç al recurs
https://en.wikipedia.org/wiki/voronoi_diagram
Exemple d’ús
Suposem que volem analitzar si la distribució d’un cert recurs està ben repartida per una àrea. Per exemple, volem saber com estan distribuïdes les farmàcies de la ciutat de Barcelona i si, més o menys, cobreixen àrees d’influència semblants en grandària i distància al centre. A partir de les posicions geolocalitzades de cada farmàcia podem generar un diagrama de Voronoi tractant-les com els centres de cada regió, i podem superposar el diagrama resultant en un mapa per veure’n la distribució espacial.
La llista de farmàcies de Barcelona i la seva posició geolocalitzada la podem obtenir, per exemple, d’un fitxer de dades obertes que publica la Generalitat de Catalunya. Després d’un processament per a resoldre els problemes detectats (un exercici interessant), suposem que tenim un fitxer amb les dades de les farmàcies de Barcelona ciutat. Llavors podem generar un diagrama de Voronoi en R i superposar-lo a un mapa generat amb leaflet també des de R:
require(leaflet)
require(ggvoronoi)
// conté almenys els camps NOM, LONGITUD i LATITUD
x=read.table("farmàcies.csv", sep=";", header=T, quote="")
// eliminar punts repetits o sense geolocalització
xxi=unique(x[x$LONGITUD!=0 & x$LATITUD!=0, c(‘LONGITUD’,’LATITUD’)])
xx=x[rownames(xxi),]
// crear el mapa
Çmapa=leaflet()
mapa=addTiles(mapa,
urlTemplate = "http://{s}.tile.openstreetmap.org/{z}/{x}/{y}.png")
// crear el diagrama de Voronoi
vvv=voronoi_polygon(xx, x='LONGITUD', y='LATITUD')
// afegir els centres al mapa
mapa=addMarkers(mapa, lng=vvv$LONGITUD, lat=vvv$LATITUD, popup=vvv$NOMENI)
// afegir els polígons generats pel diagrama de Voronoi
mapa=addPolygons(mapa, data=vvv)
// mostrar el mapa
mapa
La visualització de la variable mapa obrirà una finestra del navegador per defecte i mostrarà un mapa com el següent (una vegada ajustat el zoom):
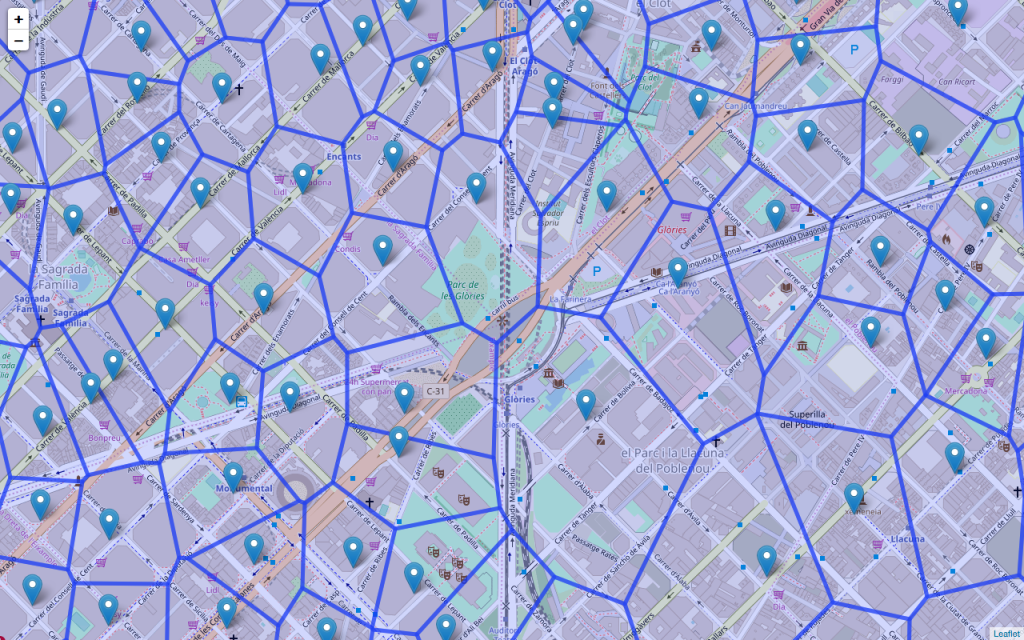
Com es pot veure, s’ha trobat l’àrea d’influència de cada farmàcia, tot i que en usar la distància euclidiana per defecte les regions creades pel diagrama de Voronoi no segueixen cap patró relatiu a l’estructura de carrers, que és quadriculada. No obstant això, el diagrama permet comprovar que hi ha zones amb una gran densitat de farmàcies, mentre que n’hi ha d’altres en què una farmàcia cobreix més territori, segurament seguint un patró relacionat amb la densitat de població (aquest seria un altre exercici interessant).
Enllaços relacionats
En Mathematica: http://mathworld.wolfram.com/voronoidiagram.html
Leaflet per a R: https://rstudio.github.io/leaflet/
El package ggvoronoi de R: https://cran.r-project.org/web/packages/ggvoronoi/index.html