Descripció
Quan analitzem xarxes (o grafs), el més habitual és començar per descriure els estadístics més senzills relacionats amb els elements de la xarxa, és a dir, nodes i arcs o arestes (depenent de si la xarxa o graf és dirigida o no, respectivament). Entre d’altres, es poden calcular els descriptors següents de manera senzilla:
- el nombre de nodes
- el nombre d’arcs/arestes
- la densitat, que és el nombre d’arcs/arestes dividit pel nombre total que podria contenir la xarxa si fos completa
- el grau en terme mitjà
Òbviament, hi ha altres descriptors més complicats que poden aportar informació sobre l’estructura interna de la xarxa, però són més complicats de calcular i d’interpretar.
Enllaç al recurs
https://zenodo.org/record/5083036
Exemple d’ús
La figura següent, creada per Martin Grandjean (@GrandjeanMartin a Twitter), mostra com quatre xarxes absolutament diferents poden compartir els mateixos descriptors, de la mateixa manera que fa l’exemple del quartet d’Anscombe. Per tant, és important visualitzar les dades (en aquest cas, la xarxa) per poder copsar-ne la naturalesa real més enllà d’aquests descriptors, ja que dues xarxes que comparteixen el mateix nombre de nodes i la mateixa distribució de graus poden ser completament diferents.
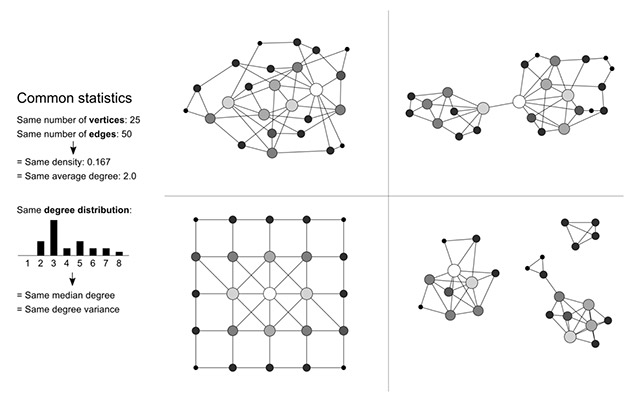
Però atenció, la visualització també pot ser mal interpretada si no es té en compte que dues xarxes idèntiques (més ben dit, isomorfes) es poden representar de manera diferent, en funció d’on se situïn els seus elements, com passa en el cas de les xarxes superior esquerra i inferior esquerra. Malauradament, saber si dues xarxes són isomorfes és un problema complicat de resoldre per a xarxes de certa mida.
Exemples com aquest s’estudien a l’assignatura Anàlisi de xarxes socials, del grau de Ciència de Dades Aplicada de la UOC.
Enllaços relacionats
Quartet d’Anscombe: https://ca.wikipedia.org/wiki/Quartet_d’Anscombe
Grafs isomorfs: https://en.wikipedia.org/wiki/Graph_isomorphism_problem
