Descripció
Aquesta entrada de blog resumeix les distribucions de probabilitat (discretes i contínues) més importants, i de cadascuna d’elles presenta una breu descripció, la gràfica amb la seva funció de densitat i les equacions que la descriuen.
No obstant això, el més interessant d’aquest recurs és el diagrama que mostra les relacions i equivalències entre les diverses distribucions de probabilitat, quan s’apliquen transformacions a una variable o més que segueixen aquesta distribució.
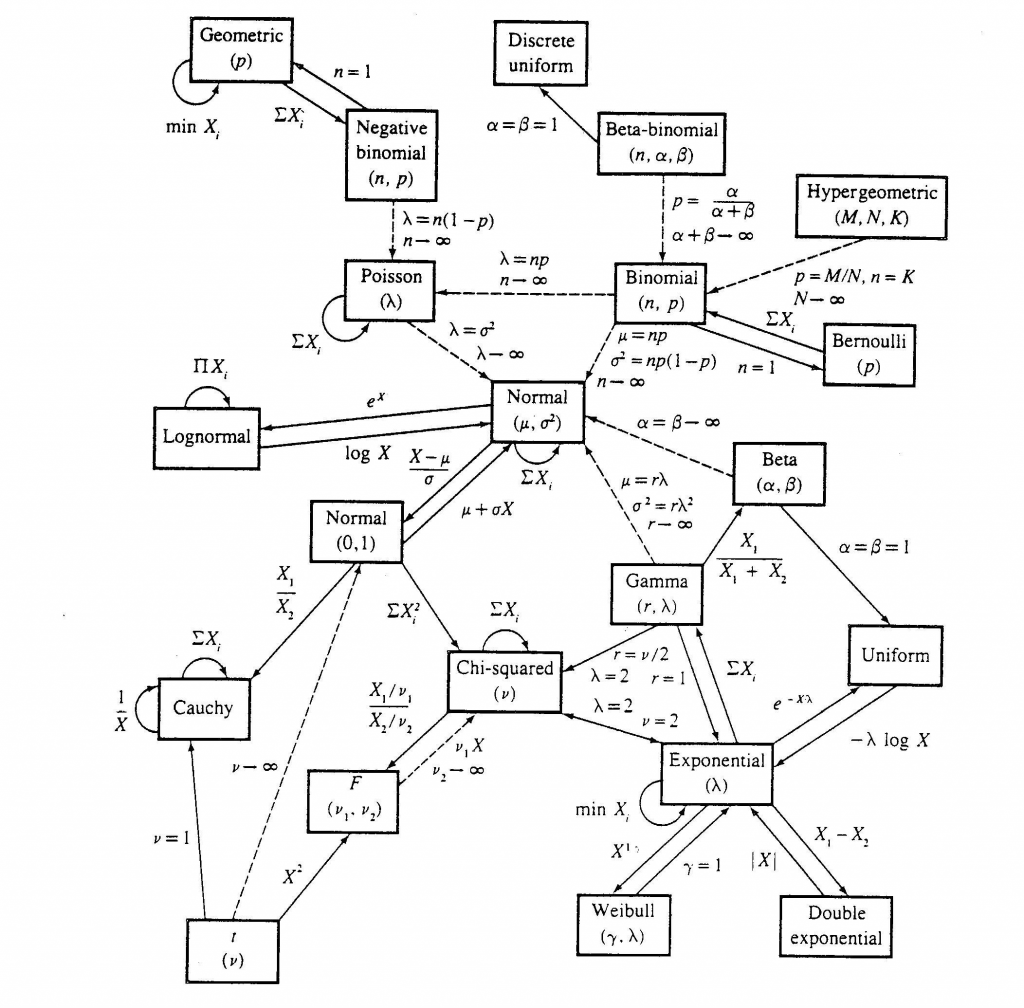Relacions entre distribucions normals. Les línies contínues representen transformacions i casos especials, les línies discontínues representen límits.
Adaptat de Leemis (1986)
Enllaç al recurs
https://medium.com/@ciortanmadalina/overview-of-data-distributions-87d95a5cbf0a
Exemple d’ús
Per exemple, pel que fa a la distribució normal amb mitjana μ i desviació típica σ, que ocupa un lloc predominant al centre del diagrama, aquest ens indica que una suma de variables aleatòries Xi que segueixen aquesta distribució normal també segueix una distribució normal, mitjançant la fletxa que va de la caixa que representa aquesta distribució a ella mateixa i etiquetada com a ∑ Xi per indicar-ho. La distribució normal està relacionada amb la distribució lognormal, de manera que el logaritme d’una variable que segueix una distribució normal és una distribució lognormal, mentre que el producte de variables que segueixen una distribució lognormal és també una variable lognormal.
D’altra banda, una distribució binomial de paràmetres n i p és (asimptòticament) equivalent a una distribució de Poisson de paràmetre λ quan es compleix que λ = np i que n tendeix a infinit (o és suficientment gran).
Enllaços relacionats
Distribució de probabilitat: https://en.wikipedia.org/wiki/probability_distribution